判断间的反对关系和矛盾关系示例
一、两个判断之间的反对关系:
反对关系包括上反对关系和下反对关系。
(1)上反对关系的含义、口诀:
上反对关系是指对于同一事物的描述,除对立的两种情况A、B之外,还存在其他情况,非此未必彼,非彼未必此,且A、B不相交,此时A、B为上反对关系。(一般地,把上反对关系默认为反对关系)
上反对关系不能同真,可以同假。若一个为真,则另一个必为假;若一个为假,则另一个真假不定。如“所有的花都是有毒的”与“所有的花都是无毒的”二者是上反对关系,它们不能同真,但可以同假。
上反对关系是“所有……是”(全称肯定判断所有S是P)和“所有……非”(全称否定判断所有S不是P)的关系,其口诀是:“两个所有,不能同真,必有一假,可以同假”。矛盾律适用于上反对关系判断。
(2)下反对关系的含义、口诀:
下反对关系是指对于同一事物的描述,只分对立的两种情况A、B,且A、B有交集,此时A、B为下反对关系。
下反对关系不能同假,可以同真。若一个为假,则另一个必为真;若一个为真,则另一个真假不定。如“有些花有毒”与“有些花无毒”二者是下反对关系,它们不能同假,但可以同真。
下反对关系的两个判断必有一真,可以同真。由其中一个判断的假,可以必然推出另一个判断的真。如由“有的金属不能导电”的假,可以必然推出“有的金属能导电”的真。
但由其中一个判断的真,却不能必然推出另一个判断的假。如由“有的金属是固体”的真,就不能必然推出“有的金属不是固体”的假。因为当其中一个判断真时,另一个判断可能为真(如当“有的金属是固体”为真时,“有的金属不是固体”也为真),也可能为假(如当“有的鲸是哺乳动物”为真时,“有的鲸不是哺乳动物”则为假)。
下反对关系是“有些……是”(特称肯定判断有的S是P)和“有些……非”(特称否定判断有的S不是P)之间的关系,其口诀是:“两个有些,不能同假,必有一真,可以同真”。排中律适用于下反对关系判断。
“有些花有毒”与“有些花无毒”二者同真,则证明“所有的花是有毒的”与“所有的花都是无毒的”二者同假。
(3)上下反对关系的真假情况:

在上表三种情况中,上反对关系(“两个所有”)是每种情况均必有一假,包括二者同假;下反对关系(“两个有些”)是每种情况均必有一真,包括二者同真。
二、两个判断之间的矛盾关系:
从判断来说,矛盾关系是指素材相同的全称肯定判断与特称否定判断、全称否定判断与特称肯定判断、单称肯定判断与单称否定判断之间的真假关系,即不可同真也不可同假的关系。如下图:
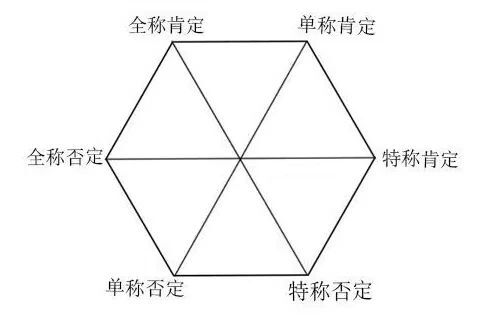
具有矛盾关系的两个判断,叫做“矛盾判断”。两个判断不能同真,也不能同假。
已知一个判断是真的,则可推知另一个判断必假。如已知“所有三角形的内角和都是180度”是真的,则可推知“有些三角形的内角和不是180度”必是假的。又如由“所有鲸都是哺乳动物”的真,必然推出“有的鲸不是哺乳动物”的假;由“所有鲸都不是卵生动物”的真,必然推出“有的鲸是卵生动物”的假。
已知一个判断是假的,则可推知另一个判断必真。如已知“所有的人都是白种人”是假的,则可推知“有些人不是白种人”必是真的。又如由“所有导电体都是固体”的假,必然推出“有的导电体不是固体”的真;由“所有导电体都不是固体”的假,必然推出“有的导电体是固体”的真。
三、全称判断、特称判断的真假情况:
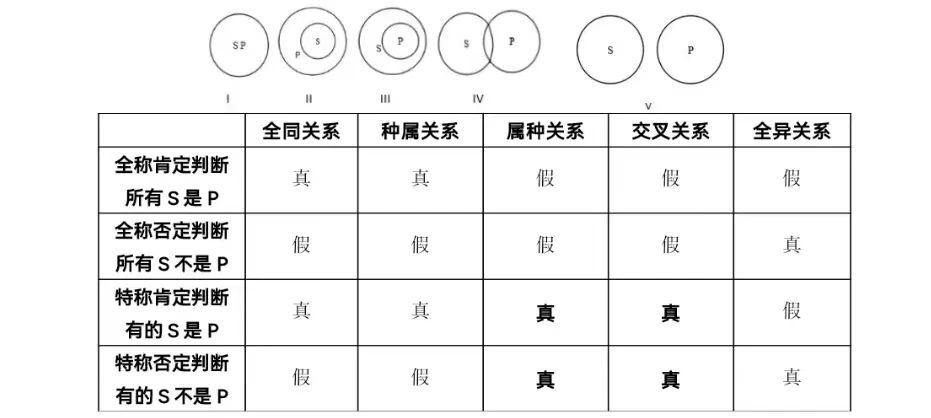
四、全称判断、特称判断与矛盾关系、反对关系:
主谓项相同的四种判断之间的关系,如下图:
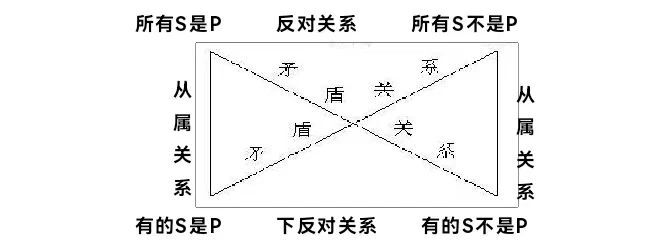
全称肯定判断与全称否定判断之间的关系,二者不能同真,一个真另一个必假,但二者可以同假,即当一个假时,另一个可真可假。这种不能同真可以同假的关系叫做上反对关系。
特称肯定判断与特称否定判断之间的关系,二者不能同假,一个假另一个必真,但二者可以同真,即当一个真时,另一个可真可假。这种不能同假可以同真的关系叫做下反对关系。
全称肯定判断与特称否定判断、全称否定判断与特称肯定判断之间的关系,二者既不能同真也不能同假。这种真假关系叫做矛盾关系。
全称肯定判断与特称肯定判断、全称否定判断与特称否定判断之间的关系,二者的关系是全称真特称必真,全称假特称真假不定;特称假全称必假,特称真全称真假不定。这种真假关系称为从属关系。
五、矛盾律与排中律的适用情况:
(1)合乎逻辑的思维要遵循矛盾律的要求:
矛盾律指明“有假”,即指明两个互相矛盾或具有上反对关系的判断,不能同真,必有一假。矛盾律适用于矛盾关系判断、上反对关系判断。
矛盾律要求人们不能同时肯定在同一时间、从同一方面、对同一对象所形成的论断A和非A,即A与非A不能同真,必有一假。恰好,上反对关系和矛盾关系不能同真,必有一假。因此,矛盾律是针对这两种关系制定的。
当我们同时肯定全称肯定判断与全称否定判断、全称肯定判断与特称否定判断、全称否定判断与特称肯定判断时就会违反矛盾律,但同时肯定特称肯定判断与特称否定判断则无妨。
(2)合乎逻辑的思维还要满足排中律:
排中律指明“有真”,即指明两个互相矛盾或具有下反对关系的判断,不能同假,必有一真。排中律适用于矛盾关系判断、下反对关系判断。
排中律要求人们不能同时否定在同一时间、从同一方面、对同一对象所形成的论断A与非A,即A与非A不能同假,必有一真。恰好,下反对关系和矛盾关系不能同假,必有一真。因此,排中律则是针对这两种关系制定的。
当我们同时否定特称肯定判断与特称否定判断、全称肯定判断与特称否定判断、全称否定判断与特称肯定判断时就会违反排中律,但同时否定全称肯定判断与全称否定判断则无妨。
(3)对具有矛盾关系的两个判断,既不可以同时肯定,也不可以同时否定:
甲:下周去香山看红叶,你去吗?
乙:谁说我不去?
甲:你去,请登记吧。
乙:我要是去,早就登记了。
在上例中,“乙去香山”和“乙不去香山”是矛盾关系。
一方面,乙既否定了不去香山,又否定了去香山,违背了排中律;而另一方面,乙既肯定了去香山,又肯定了不去香山,也违背了矛盾律。
因此,当对存在矛盾关系的两个判断进行同时肯定时也进行了同时否定,就会同时违背矛盾律和排中律。
六、矛盾关系和反对关系的比较:
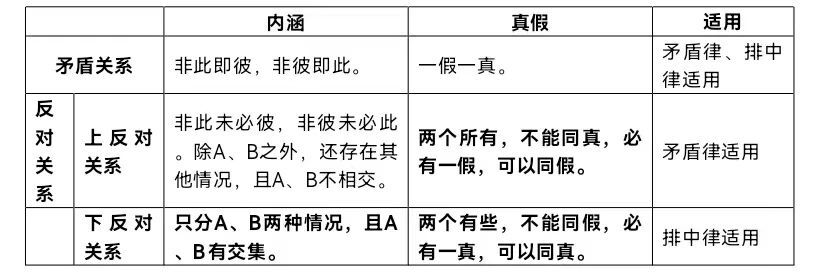
七、当两个判断没有矛盾关系时,可以用“上反对关系”或“下反对关系”来解题:
【例1】甲、乙、丙三人对某公司所有人员是否会开车做出如下推测:
甲说:该公司有人会开车。
乙说:该公司的李经理和王会计都不会开车。
丙说:该公司有人不会开车。
如果三人的推测只有一个为真,则下列哪项判断必然为真
A.该公司所有人都会开车
B.该公司所有人都不会开车
C.该公司的李经理可能不会开车
D.该公司的王会计可能不会开车
【解释】选A。甲和丙是“有些是和有些非”的关系,必有一真,则乙的话为假,得出李经理会或者王会计会,所以有些是会开车的,则甲的话为真,丙的话为假,所以人都会。
【例题2】甲、乙、丙三同学在一起议论本班参加A活动的情况:
甲说:我班所有同学都参加了;
乙说:张帆参加且李航也参加;
丙说:我班所有同学都没有参加。
已知三人中只有一人说的不正确,由此可见
A.甲说的不正确,张帆参加
B.乙说的不正确,张帆参加了
C.丙说的正确,张帆没参加
D.丙说的不正确,张帆参加了
【解释】选D。甲和丙是“所有是和所有非”的关系,必有一假,则乙的话为真,得出张帆参加且李航也参加,所以丙的话为假,所以甲为真,所有同学都参加。
【例3】“我不认为所有学生都是勤奋的,同时我也不认为所有学生都是不勤奋的。”
【解释】“两个所有”的判断是上反对关系,不能同真,必有一假,可以同假
本题前者为“所有A是B”,后者为“所有A不是B”,是上反对关系。
所有学生都是勤奋的,所有学生都是不勤奋的,二者是上反对关系,可以同时否定。因此,“我不认为所有学生都是勤奋的,同时我也不认为所有学生都是不勤奋的”,这并不违背逻辑规律。
上反对关系,可以同时否定,不违反排中律。如“我不认为所有的人都是自私的,我也不认为所有的人都不是自私的”,因为它所否定的两个判断是同一素材的全称肯定判断和全称否定判断,它们之间是上反对关系。

